多层线性模型(Hierarchical Linear Model,HLM),也叫多水平模型(Multilevel Model,MLM),是社会科学常用的高级统计方法之一,它在不同领域也有一些同近义词和衍生模型:
线性混合模型(Linear Mixed Model) 本文分为两个部分:
1. 什么是HLM(入门科普)
2. HLM的自由度计算问题(进阶探讨)
1 / 什么是HLM 子曾经曰过:"HLM是众多统计方法的幕后主使。" 什么意思呢?一般我们收集完数据之后会做什么分析?做实验的人可能会说:方差分析(ANOVA);做调查的人可能会说:多元回归(multivariate regression);做文献综述的人可能会说:元分析(meta-analysis)……但其实,这一切都可以视为HLM的特例:
t检验是ANOVA的一个特例 简而言之:回归分析是几乎所有统计模型的基础,而回归分析的最一般形式则可以进一步归为多层线性模型HLM 。
当然,除去上面这些HLM的特例,HLM本身关注的焦点其实是"多层嵌套数据" 。
举个栗子,假设我们想知道"智力水平(IQ)能否影响学业成绩(GPA)",然后我们收集了很多很多学校的数据,迫不及待地画了一个散点图:
一般线性模型(GLM),即最普通的回归分析 这样一看,IQ和GPA并无什么关系呀,甚至还有一点负相关?!于是我们就下结论"IQ与GPA无关"吗?emmm等等,我们漏了什么?
事实上,不同学校之间在很多方面可能都存在固有的差异,比如学生整体的智力情况、教学条件、师资力量等等。现在考虑一个最简单也最极端的情形:收集的学校里面既有"精英学校"也有"差劲学校",学生入学的标准就是他们的IQ(当然,如此把学生分成三六九等是很不好的!这里只是为了方便理解)。
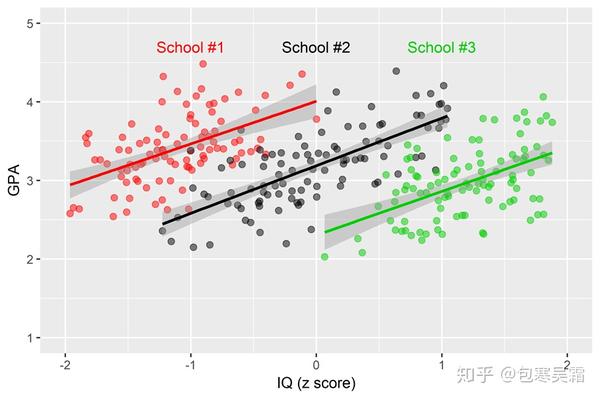
然后我们重新对不同学校分别画一下散点图:
多层线性模型(HLM) 你会发现,如果考虑了学校间的固有差异,或者说"基线水平"差异,IQ和GPA之间的关系就不会受到这些因素的混淆了(咳咳,这里的数据都是我瞎编的啊,别当真)。以上就是经典的"组内同质、组间异质" 的情况,我们刚刚做的其实就可以视为HLM的其中一种子模型——随机截距-固定斜率模型,也就是假定不同学校的基线水平不同(随机截距),但IQ与GPA之间的变量关系在不同学校中保持相同(固定斜率)。
HLM会把多层嵌套结构数据在因变量上的总方差进行分解:
总方差 = 组内方差(Level 1)+ 组间方差(Level 2)
——咦,你是不是联想到了方差分析?没错!比如在上面的例子中,学生是个体水平(Level 1)的分析单元,IQ和GPA都是在个体水平收集的变量,而学校是群体水平(Level 2)的分析单元,不过我们暂时并没有收集学校水平的任何自变量,只是把学校本身当做一个分组变量(clustering/grouping variable) 。换句话说,上面这个例子也可用被称作"随机效应单因素协方差分析(ANCOVA with random effects) "。
现在用公式来表示上面这个例子:
我们既可以用R语言lme4包的lmer函数,也可以用SPSS的MIXED语句进行建模:
# R语言 - 固定斜率: model = lmer ( GPA ~ IQ + ( 1 | School ), data = data ) # SPSS - 固定斜率: MIXED GPA WITH IQ / METHOD = REML / PRINT = DESCRIPTIVES SOLUTION TESTCOV / FIXED = IQ | SSTYPE ( 3 ) / RANDOM = INTERCEPT | SUBJECT ( School ) COVTYPE ( VC ) . 或者可以设置IQ为随机斜率(即理论上假定IQ与GPA之间的关系在不同学校是不一样的):
# R语言 - 随机斜率: model = lmer ( GPA ~ IQ + ( IQ | School ), data = data ) # SPSS - 随机斜率: MIXED GPA WITH IQ / METHOD = REML / PRINT = DESCRIPTIVES SOLUTION TESTCOV / FIXED = IQ | SSTYPE ( 3 ) / RANDOM = INTERCEPT IQ | SUBJECT ( School ) COVTYPE ( UN ) . 当然,我们还可以引入学校水平的自变量来对学校间的GPA均值差异进行解释,比如教师数量、教学经费……这些变量由于只在 学校层面变化,对于每个学校内的每一个学生而言都只有 一种可能的取值,因此必须放在Level 2的方程中作为群体水平自变量,而不能简单地处理为个体水平自变量——这也就是HLM的另一个存在的意义:可以同时纳入分析个体与群体水平的自变量 。
我们来看HLM的一般式:
Level 1(组内/个体水平,或重复测量/追踪设计中的时间水平;p个自变量,i个样本量):
Level 2(组间/群体水平,或重复测量/追踪设计中的个体水平;q个自变量,j个样本量):
以上就是关于HLM的入门级科普。我不确定是不是所有读者都对HLM有足够的了解,因为很多同学其实是没有接触过HLM的,我自己也是去年暑假才开始学习HLM。不仅如此,一些实验取向、认知取向的同学甚至会怀疑回归分析的意义,因为在他们的研究中,t检验和ANOVA就足够用了——而这些分析的本质其实都是回归分析,回归分析的更一般形式则是HLM。另外也有不少同学把"多层线性模型"与"分层(逐步)多元回归"搞混淆 ——请注意:HLM解决的是多层嵌套结构数据(落脚点是数据结构 ),而分层(逐步)多元回归本身是普通的回归分析,解决的是不同自变量的重要性的优先程度(落脚点是变量重要性 )。
2 / HLM的自由度计算问题 前面这些都只是铺垫,因为下面的内容才是重点。我们来谈谈HLM的自由度计算问题 。
自由度(degree of freedom, df ) ,简单来说就是"能够独立变化的数据量" 。比如一组有N 个数据的样本,其总体平均值是确定的,那么在参数估计中,我们说它的自由度是N – 1,这里的1代表已经确定了的均值,也就是说无论你的数据怎么变,只要给我N – 1个数,我就能知道剩下的那个数是几,因为均值已经确定了。
而在普通的回归分析中,同样道理,截距相当于一个已经确定了的均值,是我们要估计的一个参数,并且每增加一个自变量,都会相应增加一个回归系数,这些回归系数也是我们要估计的参数,也视为确定值,因此剩下的那些不确定的、能够独立变化的数据的个数就是自由度,主要用于假设检验(对回归系数的检验:t = b/SE ,服从df = N – k 的t 分布,其中N 为总样本量,k 为所有的参数个数,截距也占一个参数) 。
一言以蔽之:
df (能够独立变化的数据量)= N (总数据量)– k (待估计的参数个数 [包括截距])事实上任何一个回归方程都有且仅有一个截距,就好比任何一组数据都有且仅有一个平均值,所以很多时候上面这个表达式也可以用"自变量/预测变量"的个数来表示:
df = N – k = N – p – 1(p 表示自变量/预测变量的个数,1表示截距这个参数)
然而,这么一目了然的事情在HLM里面却是一件比较复杂的议题 ,因为前面我们已经看到,HLM的回归方程不止一个,不仅有Level 1的一个方程,还有Level 2的一系列以Level 1的每个参数(包括截距和斜率)为因变量建立的方程,因此不同的回归系数因其对应的变量有不同的性质(或者说在HLM中所处的不同层级),其自由度也不尽相同 。
你可能要问了:
HLM的自由度真的是一个问题吗? 我相信不仅是我自己有这样的疑问,各位读者也会产生类似的疑问。我遇到HLM自由度的问题也是在前不久,在使用R语言的lme4包和lmerTest包做HLM的时候,lmerTest输出的某个Level 2自变量的自由度(20多)远远小于它本身的Level 2样本量(400多),非常离谱,并且我做的所有模型的自由度都是小数而不是整数。无独有偶,室友 @张了了 也遇到了HLM自由度的问题(混合线性模型(LMM)中,固定效应(Fixed Effects)中的自由度是如何计算的? )。
碰巧,我这几天查了很多参考书和文献,终于把HLM的自由度问题给搞清楚了!
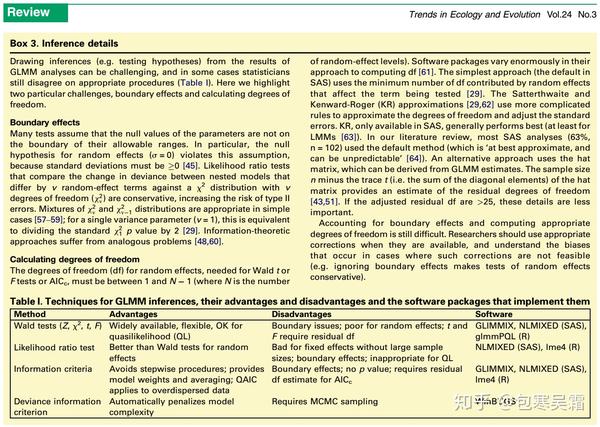
Q1:HLM自由度的计算真的是一个争议问题吗? 是的,不要小看它!我们先来看一篇2009年发表在《Trends in Ecology and Evolution》上面的综述文章「Generalized linear mixed models: A practical guide for ecology and evolution」。
文章提到:不同软件在计算HLM自由度的时候,差异非常之大(vary enormously),HLM自由度的计算目前仍然是一个challenge和difficulty 。
Bolker et al., 2009 Q2:目前有哪些计算HLM自由度的方法?我该如何选择? 大体分两类:"简单计算法" 和"近似估计法" 。
在综合了很多中英文教材之后,我把它们归纳如下:
HLM自由度算法总结 HLM自由度算法总结(一览表) 常见自由度类型举例 总结:
HLM软件(软件本身叫做HLM)作为最经典的HLM统计工具,输出的都是由"简单计算法"估计的自由度,并且都是整数,不存在小数。这种方法理解起来也很简单,就是我们上面提到的原则:df (能够独立变化的数据量)= N (总数据量)– k (待估计的参数个数 [包括截距])注意:当level-1的某变量被设定为随机斜率,df计算略复杂,可参考上面的Table 1 理论驱动 的方法。 SPSS和R语言的lmerTest包均默认输出Satterthwaite(1946)的自由度近似估计值(approximation),这种算法是基于每一个变量在不同level的残差方差(residual variances)做的校正估计 ,严格来说是一种数据驱动 的方法,主要用于校正方差不齐/异方差、每组内样本量不均衡、组数量较少 等情况。这种近似估计往往得不到整数,而是会出现小数,但正常情况下,估计出来的自由度与简单计算法也是处于同一个数量级的,不会偏差太多。而当每组内样本量相等时,Satterthwaite的近似估计自由度与简单计算法得到的自由度就是一致的了,并且都是整数。 R语言的lmerTest包,除了Satterthwaite近似估计,还提供了Kenward-Roger近似估计,但后者不如前者好用(比如百万数量级的数据如果用KR估计就会直接崩溃)。 R语言的lme4包(最根源的HLM程序包,lmerTest只是调用了它并增添了假设检验结果)早期也会报告自由度和假设检验结果,但后来取消了这一功能,我推测可能是因为HLM自由度的估计尚存争议,所以希望用户自己来选择使用哪种自由度。 Q3:选择哪种自由度真的很重要吗? 在明白了上面的理论问题之后,我就自编了一个R函数,从而可以实现像HLM软件那样自己根据理论假设去设定每个变量/参数的类型(如intercept、L1 fixed、L1 random、L2、cross-level interaction),分别计算不同类型的df,并输出假设检验结果和效应量。在实际分析了自己的数据之后,我发现虽然"简单计算法"和"近似估计法"对df的估计有时确实相差挺多,但显著性检验的结果(p值)基本是一致的 ,这可能是因为我的数据里Level 2的group数量已经很多(几百或几千),即使df有校正,影响也微乎其微。
# 前半部分是lmerTest的输出(t-tests use Satterthwaite's method) # 最后四列是我自编函数的输出(简单计算法) # p值其实是基本一致的,但df差别很大 # # Fixed effects: # Estimate Std. Error df t value Pr(>|t|) df p r sig # (Intercept) -0.856254 0.018742 133 -45.687 2.79e-83 NA NA NA <NA> # NU 0.033832 0.001650 2435 20.504 2.57e-86 1912 1.30e-84 0.42456 **** # CCU 0.008637 0.001462 1047 5.906 4.74e-09 1912 4.15e-09 0.13384 **** # NV 0.030872 0.002143 1323 14.409 7.90e-44 1912 9.24e-45 0.31296 **** # NG -0.011341 0.002069 849 -5.481 5.58e-08 1912 4.79e-08 -0.12437 **** # SNU -0.002959 0.001433 137 -2.065 4.08e-02 491 3.94e-02 -0.09280 * # SNI 0.000019 0.000126 109 0.151 8.81e-01 491 8.80e-01 0.00679 # sex -0.092968 0.001107 2933435 -83.949 0.00e+00 3141569 0.00e+00 -0.04731 **** # age -0.000424 0.000069 2436232 -6.144 8.06e-10 3141569 8.06e-10 -0.00347 **** # edu 0.143061 0.000344 3071119 415.565 0.00e+00 3141569 0.00e+00 0.22827 **** # exp -0.027545 0.000243 3124714 -113.187 0.00e+00 3141569 0.00e+00 -0.06373 **** # salary -0.021957 0.000480 3139637 -45.787 0.00e+00 3141569 0.00e+00 -0.02582 **** 然而,如果使用"t-to-r"转换来计算multilevel效应量,那么df的差异就很要命了,因为r = sqrt(t^2/(t^2+df)),df会直接影响最后算出来的效应量(Satterthwaite常常会低估df,使得效应量被高估)。
所以!自由度的估计方法,对显著性检验(p值)的影响其实并不大,但是对效应量计算(如t-to-r转换)的影响很大。
我个人的选择是:用R作为统计工具(因为SPSS跑大数据模型实在太吃力了),依然使用lme4和lmerTest包,但在自由度方面还是遵循HLM软件所使用的简单计算法,同时也看一眼lmerTest输出的Satterthwaite校正结果,双重保障。
附件:HLM df.pdf (关于HLM自由度问题的笔记和总结)
参考文献: Bolker, B. M., Brooks, M. E., Clark, C. J., Geange, S. W., Poulsen, J. R., Stevens, M. H. H., & White, J.-S. S. (2009). Generalized linear mixed models: A practical guide for ecology and evolution. Trends in Ecology and Evolution, 24 (3), 127–135.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah, NJ: Erlbaum.
Heck, R. H., Thomas, S. L., & Tabata, L. N. (2014). Multilevel and longitudinal modeling with IBM SPSS (2nd ed.). New York, NY: Routledge.
Hox, J. J. (2010). Multilevel analysis: Techniques and applications (2nd ed.). New York, NY: Routledge.
Satterthwaite, F. E. (1946). An approximate distribution of estimates of variance components. Biometrics Bulletin, 2 (6), 110–114.
Snijders, T. A. B, & Bosker, R. J. (2012). Multilevel analysis: An introduction to basic and advanced multilevel modeling (2nd ed.). London: Sage.
郭志刚 等译. (2016). 分层线性模型: 应用与数据分析方法 (第2版). 北京: 社会科学文献出版社.
温福星. (2009). 阶层线性模型的原理与应用 . 北京: 中国轻工业出版社.
谢宇. (2013). 回归分析 (修订版). 北京: 社会科学文献出版社.
郑冰岛 译. (2016). 多层次模型 . 上海: 格致出版社.
如何理解统计学中「自由度」这个概念?
统计量–效应量的相互转换 | 元分析基础
来源:知乎 www.zhihu.com
作者:
包寒吴霜 【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。
点击下载 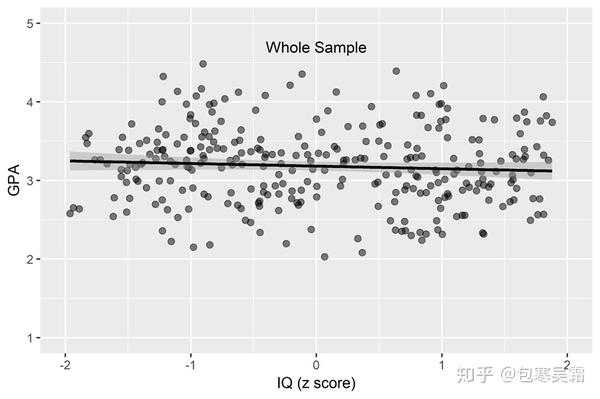




没有评论:
发表评论