之前在"复数,通往真理的最短路径"中说过,复数域其实就是二维的数域,提供了更高维度的、更抽象的视角。本文来看看,我们是怎么从实数域扩展到复数域的。
大家可能觉得这个扩展并不复杂,也就是 、
、 两个任意实数,外加虚数
两个任意实数,外加虚数 ,把它们结合在一起,就完成了:
,把它们结合在一起,就完成了:

但数域的扩张从来没有这么简单,就好像夫妻生下小孩只是个开始,困难的是之后的抚养、教育:

复数域的扩张充满崎岖。正如欧拉的老师对他的赞扬:
我介绍数学分析的时候,它还是个孩子,而你正在将它带大成人。----约翰·伯努利
这句话虽然是说微积分(数学分析)的,但用在复数域上也不违和。欧拉的欧拉公式正是"复数域"的成人礼:

1 数域扩张的历史
来看看之前的数域是怎么扩张的吧。每次想到数域的扩张,我都有种大爆炸的画面感,宇宙从一个奇点爆炸中产生:

1.1 自然数到整数
数学刚开始也是一片空白:

0的出现就是数学的奇点:

根据皮亚诺定理(可以参考为什么1+1=2?)"爆炸"出了自然数域(可以参考自然数是否包含0?):

很显然上面的图像是不对称的,哪怕出于美学考虑,人们都有冲动把左边补齐,增加负数,这样就得到了整数域:

添加负数之后,有一个问题就出现了:

我们知道 是对
是对 的缩写,并且容易推出如下计算规则:
的缩写,并且容易推出如下计算规则:

我们添加负数之后,希望这个规则依然适用,即:

更一般的有:

并且还惊喜地发掘出负数次方的意义,如果说正数次方是对乘法的缩写,那么负数次方(正数的相反数)是对除法(乘法的逆运算)的缩写:

1.2 整数到实数
很显然整数之间还有很多空隙,我们可以用有理数(rational number,翻译为"可比数"更合理):

来填满这些空隙(示意图):

还有空隙,最终用无理数(irrational number,"不可比数")来填满这些缝隙,得到实数轴:

自然会有这么一个问题:

 是无理数,上面这个问题需要用极限来回答,这里不再赘述,只是可以看出实数域的扩张也是很艰难的。
是无理数,上面这个问题需要用极限来回答,这里不再赘述,只是可以看出实数域的扩张也是很艰难的。
2 复数基础
往下面讲之前,稍微复习下复数的一些基础知识。如果比较了解复数的运算法则了,可以跳到第三节去阅读。
2.1 复数的运算规则
复数的运算规则并非凭空捏造的。开头提到的文章"复数,通往真理的最短路径"说过,形如:

的三次方程,卡尔丹诺在《大术》这本书中给出了通解:
![x=\sqrt[3]{q+\sqrt{q^2-p^3}}+\sqrt[3]{q-\sqrt{q^2-p^3}}\\](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_v1Itk22FtCBnm5bzomc8CMfD-nfkirVWq-rT8cJAq9RfMY4pDGIGCu5hipNg88ahvdtHS3IGMFO8gppp0q8qOgS39KUWjiT25owWwfbV0iDX0lNRAfcKdniQU4Eb2UgTFXfbspUFiwMIqZEj3p87kuOUHtF2r_aBKLFKWbW01Y8FZNb3X5z2EYLsxPjq7uq58t6eAAKah40HByagdezjB6lDNIMgZHInIW_QZzo5bESpM=s0-d)
如果 、
、 ,可以得到方程:
,可以得到方程:

从图像上看, 与
与 有三个交点的:
有三个交点的:
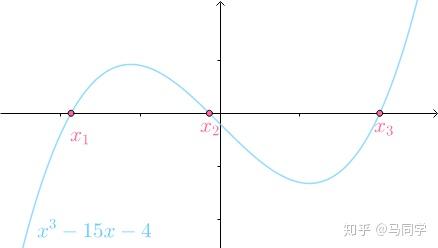
套用通解会得到:
![x=\sqrt[3]{2+\sqrt{2^2-5^3}}+\sqrt[3]{2-\sqrt{2^2-5^3}}=\sqrt[3]{2+11i}+\sqrt[3]{2-11i}\\](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_t-nFoBuZgUPsoF7XZucYAO1g2xNGH230SjD5V43Fmcuf7ya_z8h_rzM4YIwENYWCGHqKx8RpiA9FlGHdzOw8IoBHAzTijNX67ICmSzE0XWKYTEVmNnkJHQshPKM1mAdI-iR978rliMpplssIoNR_-EKb16DiZqxOlq9C44zxmzJNn5Om1YxyPgVLhaXSolV3h_ARnDR2Cz6g98vCNRxfdmOrobmPQPvf5IdcHFMCYyVjtEfZ8IZOlO7SrGTwsuFFEgQ0SiIIT4XYd3_DhRJv6gZ0edI-wABHUaAWmbySy2ss7yvpY5dxpwoUQ=s0-d)
这里就出现复数了。拉斐尔·邦贝利(1526-1572),文艺复兴时期欧洲著名的工程师,给出了一个思维飞跃,指出如果复数遵循如下的计算规则:


那么就可以根据之前的通解得到三个实数解。
2.2 复数加法、减法的几何意义
为了之后的讲解,先引入几个符号,对于一般的向量 有:
有:

复数的几何表示和二维向量有点类似,只是横坐标是实轴( ),纵坐标是虚轴(
),纵坐标是虚轴( ),下图还把刚才的符号给标了出来:
),下图还把刚才的符号给标了出来:
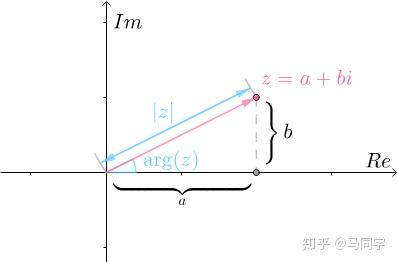
加法的几何意义和向量也一样:
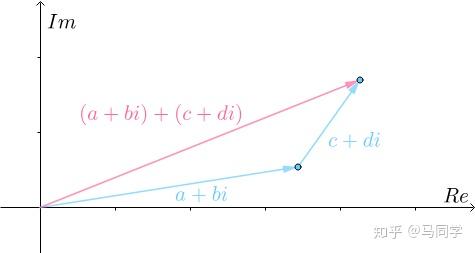
但向量没有乘法(点积、叉积和实数乘法不一样),这就是复数和向量的区别。复数是对实数的扩展,所以要尽量兼容实数,必须要有加减乘除、乘方开方、对数等运算。
根据刚才的乘法规则,计算可得:

画出来发现,两者是正交的:
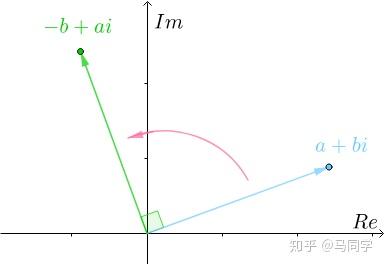
还可以从另外一个角度来理解这一点, 在复平面上是这样的:
在复平面上是这样的:
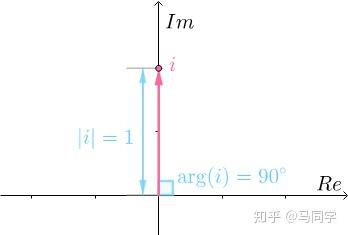
那么, 乘以虚数
乘以虚数 ,就是:
,就是:

对于一般的向量 ,也符合这个规律:
,也符合这个规律:

好了,知道这些差不多了,开始正题。
3 复数域的扩张
好了,轮到复数域了,复数定义为:

那么,来回答数域扩张都会问到的问题吧:

这个问题可以用欧拉公式:

来回答,取 ,可得:
,可得:

画出来就是复平面上模长为1,幅角也为1的点:
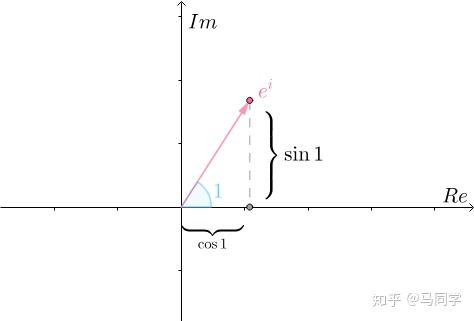
更一般的,欧拉公式说明, 是单位圆上幅角为
是单位圆上幅角为 的点:
的点:
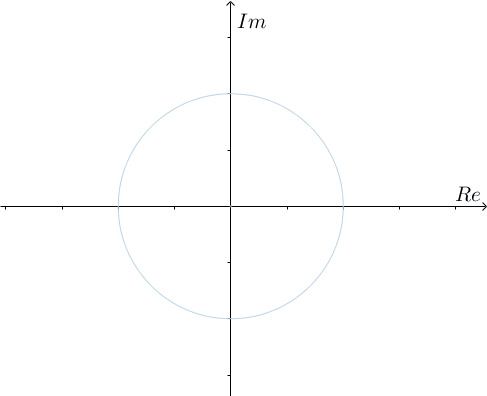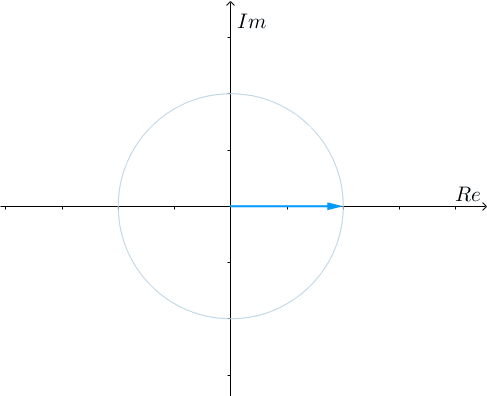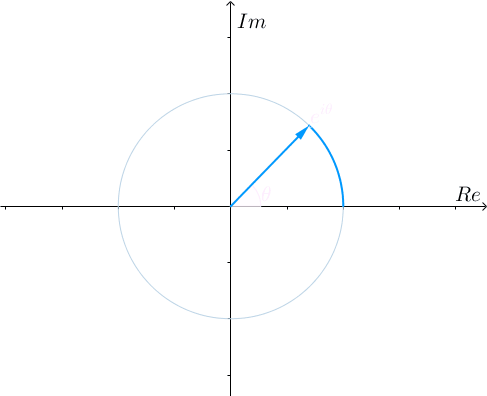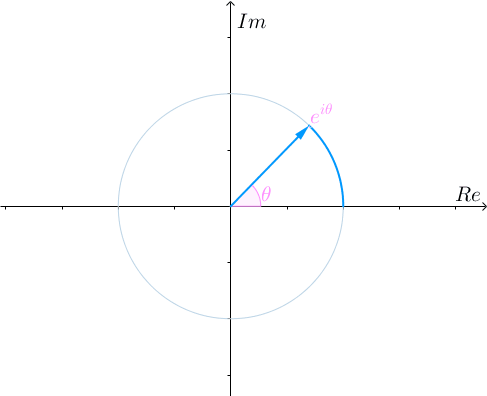
但是,欧拉公式 长这个样子!
长这个样子!
3.1  的定义
的定义
欧拉公式肯定不是凭空捏造的,先来看看实数域中有什么可以帮助我们的。
实数域中的 函数,起码有三种定义方式:
函数,起码有三种定义方式:



从这三种定义出发都可以得到欧拉公式。
3.1.1 极限的方式
因为:

我们可以大胆地令 :
:

那么之前的 就等于:
就等于:

我们来看看这个式子在几何上有什么意义。因为 对应的是单位圆上幅角为
对应的是单位圆上幅角为 的点,所以先给个参照物,虚线是单位圆,实线对应的幅角为
的点,所以先给个参照物,虚线是单位圆,实线对应的幅角为 :
:
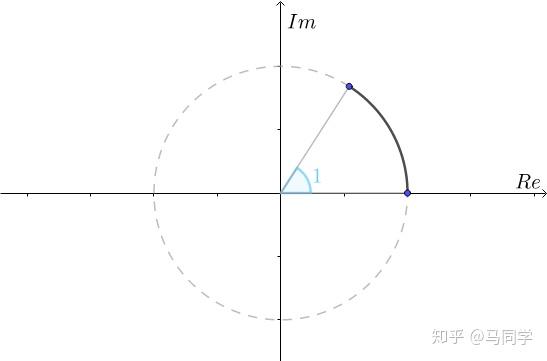
然后取 ,可以得到:
,可以得到:

根据复数的乘法规则,可以看出:
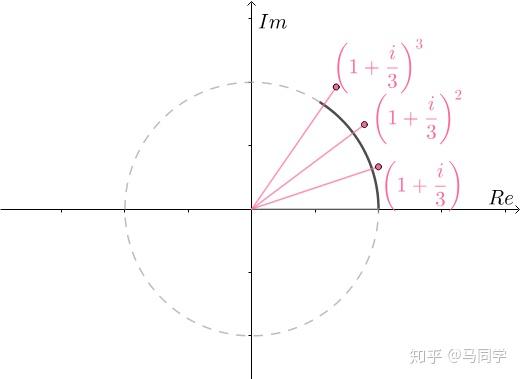
取 :
:
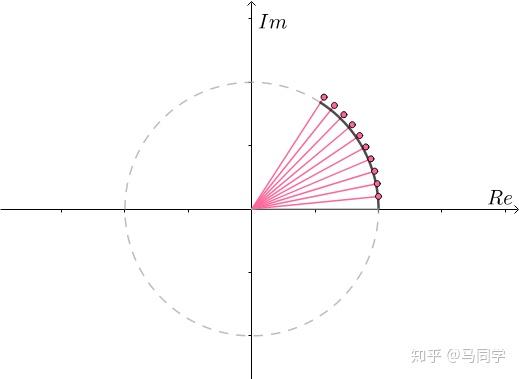
取 ,已经很接近单位圆上幅角为1的点了:
,已经很接近单位圆上幅角为1的点了:
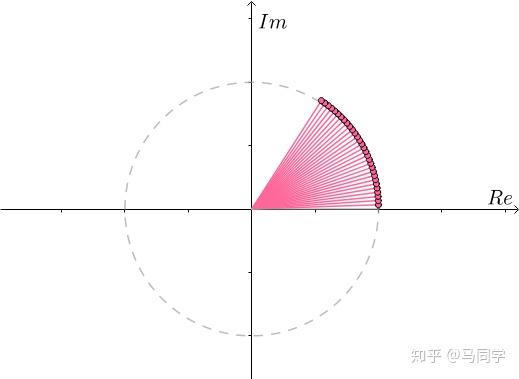
对于更一般的 也是同样的:
也是同样的:
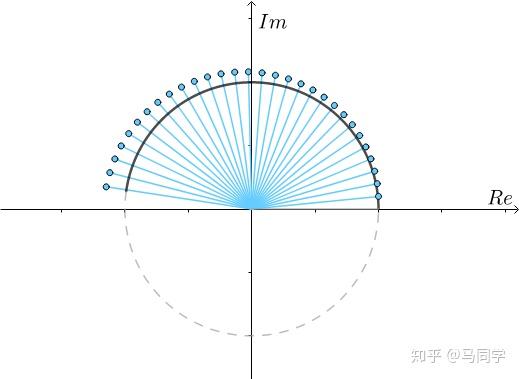
当 时,就很接近单位圆上幅角为
时,就很接近单位圆上幅角为 的点了:
的点了:
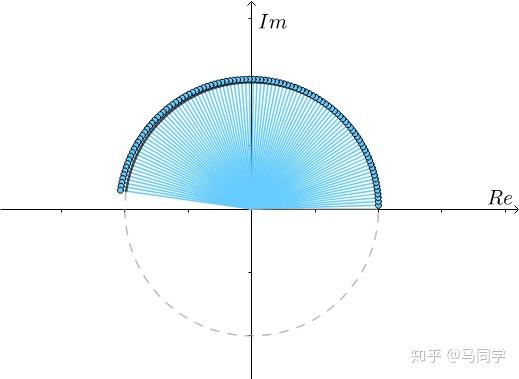
可以证明当 时,
时, 为单位圆上幅角为
为单位圆上幅角为 的点,也就是得到了欧拉公式:
的点,也就是得到了欧拉公式:

可能你还会问,直接替换 为
为 ,合理吗:
,合理吗:

这里是理解欧拉公式的 ,我们要意识到一点,欧拉公式是一种人为的选择,完全可以不这么去定义
,我们要意识到一点,欧拉公式是一种人为的选择,完全可以不这么去定义 。但是,做了别的选择,会面临一个问题:会不会在现有的庞大复杂的数学体系中产生矛盾?
。但是,做了别的选择,会面临一个问题:会不会在现有的庞大复杂的数学体系中产生矛盾?
打个比方吧,在实数中"除以 "是不合理的,假如你想让它变得合理,那么分分钟会导出矛盾:
"是不合理的,假如你想让它变得合理,那么分分钟会导出矛盾:

欧拉公式并不会引发冲突,并且随着学习的深入,你会发现数学家已经证明了它是一种足够好的选择,这里就不赘述了。
3.1.2 泰勒公式的方式
实数域下,有这些泰勒公式:



也是直接替换 ,令
,令 有:
有:

这也有漂亮的几何意义,看看 的前三项:
的前三项:

这是三个复数相加,加出来就是:
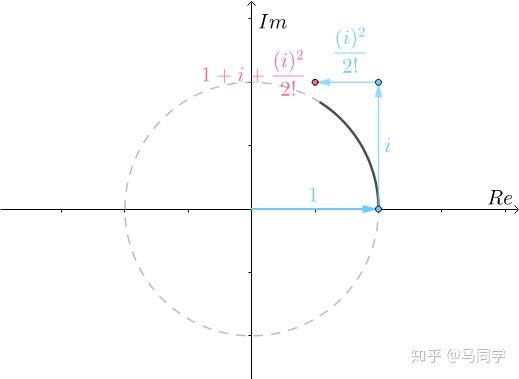
再增加第四项 :
:
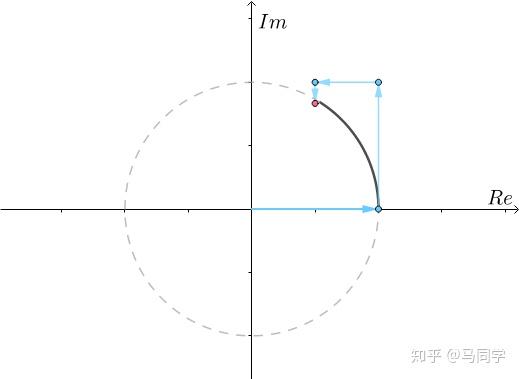
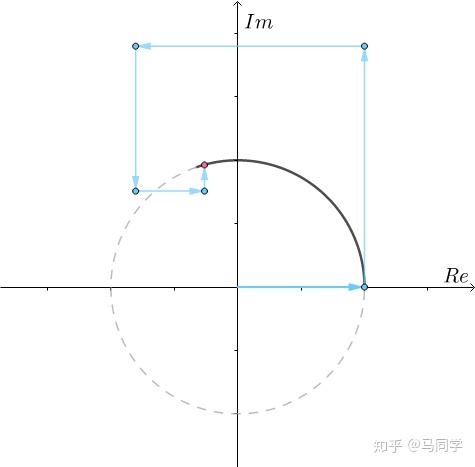
随着 ,仿佛一个螺旋不断地接近单位圆上幅角为
,仿佛一个螺旋不断地接近单位圆上幅角为 的点。对于更一般的
的点。对于更一般的 也是类似的螺旋:
也是类似的螺旋:
3.1.3 导数的方式
实数域有;

直接套用:

假设 是时间,那么
是时间,那么 是运动在复平面上的点的位移函数,
是运动在复平面上的点的位移函数, 时位置为
时位置为 :
:
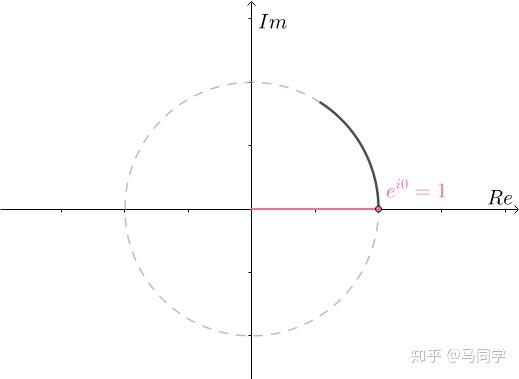
 的运动速度,也就是导数
的运动速度,也就是导数 。这个速度很显然是一个向量,有方向,也有速度。它的方向垂直于
。这个速度很显然是一个向量,有方向,也有速度。它的方向垂直于 (根据乘法规则,乘以
(根据乘法规则,乘以 表示旋转
表示旋转 ):
):
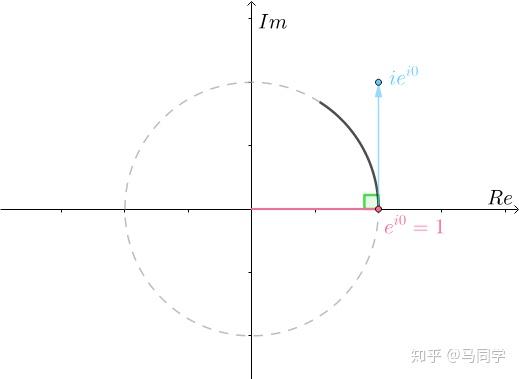
并且不论 等于多少,运动方向都垂直于位移,所以只能在单位圆上运动(圆的切线始终垂直于半径):
等于多少,运动方向都垂直于位移,所以只能在单位圆上运动(圆的切线始终垂直于半径):
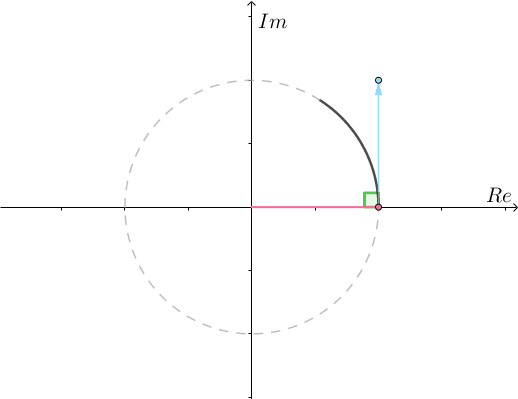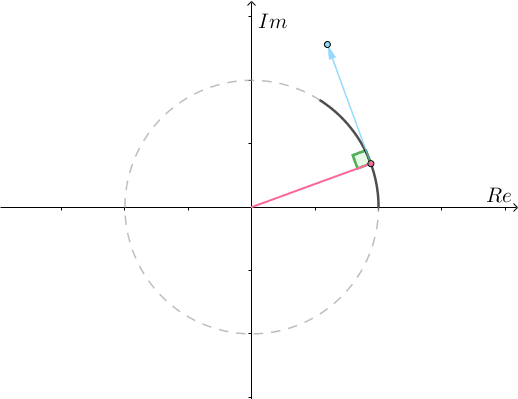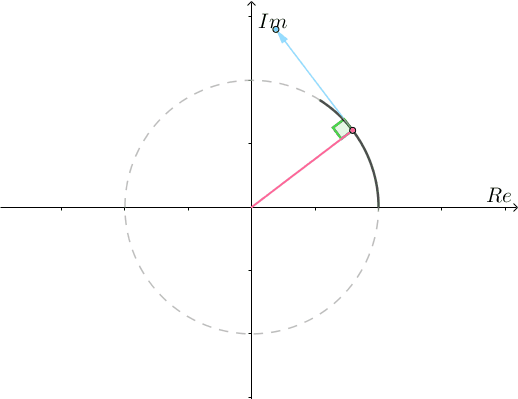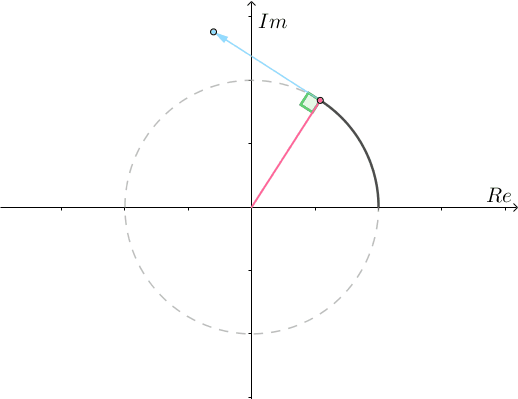
而速度的大小就是速度的模长 。之前说了,对于两个复数
。之前说了,对于两个复数 ,它们的模长为
,它们的模长为 ,那么:
,那么:

 肯定等于1了,
肯定等于1了, 在单位圆上运动,所以模长也为1,所以速度的大小为:
在单位圆上运动,所以模长也为1,所以速度的大小为:

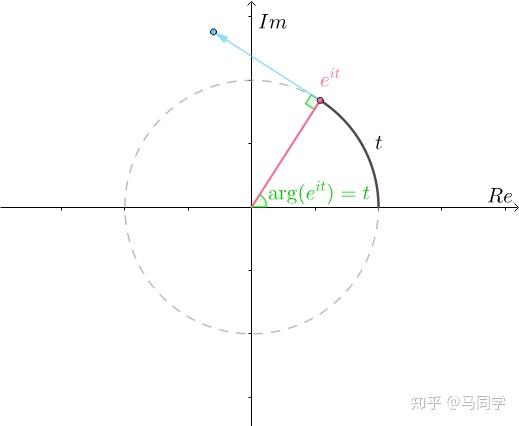
速度大小为1意味着 时刻走了
时刻走了 长度的路程。而
长度的路程。而 在单位圆上运动,那么
在单位圆上运动,那么 时刻运动了
时刻运动了 弧长,因为是单位圆,所以对应的幅角为
弧长,因为是单位圆,所以对应的幅角为 :
:
4 总结
有了欧拉公式之后,任何复数都可以表示为:

其中:

个人觉得 只是复数的初始形态,而
只是复数的初始形态,而 才是复数的完成形态,因为它更具有启发性。比如计算乘法的时候:
才是复数的完成形态,因为它更具有启发性。比如计算乘法的时候:

那么有:


几何意义更加明显。并且扩展了乘方和对数运算:


到此为止,基本上所有的初等运算都全了。更多高等的运算比如三角函数、积分、导数,也需要借助欧拉公式在复数上进行推广。
欧拉公式中,如果取 ,就得到了欧拉恒等式:
,就得到了欧拉恒等式:

这个公式也被誉为了上帝公式,包含了数学中最基本的 、
、 、
、 、
、 、
、 ,仿佛一句诗,道尽了数学的美好。
,仿佛一句诗,道尽了数学的美好。
最新版本(可能有后继更新):欧拉公式,复数域的成人礼
来源:知乎 www.zhihu.com
作者:
马同学 【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。
点击下载



























没有评论:
发表评论