作为一名研究Quantum monte carlo(QMC)的博士生,我给大家详细介绍一下这个问题。
1,为什么会有QMC?
那是因为,在经典的物理模型里,系统的状态数目随着系统的大小,是呈现指数增加的。比如Ising模型,一个阵点,自旋的方向有上或者下两种状态,两个阵点,就是四种,三个粒子就是八种.......海森堡模型或者hubbard模型也是同样的道理。
这样的物理模型,假设状态数为M,想要得到精确的结果,就需要用对角化(ED),也就是求解一个M阶矩阵。现在的计算机,求解成千上万阶的矩阵都没有问题,但是再大,时间就变的非常非常的长。例如一个4X8的二维Ising模型,状态数就达到43亿,而4X8的模型在科研人员的眼里是小的不能再小的模型!因此,用对角化的方法求精确解就变的不太现实。
因此,常见的方法就是用蒙特卡洛抽样的方法,我们不用穷尽你所有的态,只需要选取一部分具有代表性的态进行抽样即可。这样就可以大大减小计算强度,把算法从指数增长变成多项式增长,使得求解更大的系统成为可能。这就是量子蒙特卡洛的由来。蒙特卡洛方法的原理,大家可以参考我这个回答。
计算物理到底是一个怎样的专业?
当然,还有其他的解决这个问题方法,比如平均场近似(将其他粒子对该粒子的作用看成是一个场),DMRG(把系统不断的进行重整化,然后只保留可能包含基态的部分,剩下的统统丢弃),这些方法都有自己的优势和不足,就不再我的讨论范围之内了。
2,sign problem是如何出现的?
量子蒙特方法求解一个模型的某个物理量O(比如某处的自旋,关联函数,系统的基态能量等等),实际上就是对这个物理量进行抽样,然后加权平均,也就是下面这个式子。
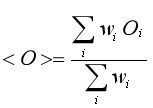
这里O(i)是测量值,而w(i)是对应的权重。
但是,这里的权重有可能是负数,特别是在费米子的计算中,由于反对称性,分母中的权重很可能正负相抵,从而使分子分母都接近0,蒙特卡洛抽样变的没有意义。
为什么权重会出负数呢。我们用一个实例来说明一下。
比如,求hubbard模型的基态。hubbard模型是凝聚态物理一个非常重要的模型,它让电子在网格中自由hoping,由于泡利不相容原理,相同自旋的电子不能呆在同一个格点,而由于库伦排斥,不同自旋的电子呆在同一个格点,会产生排斥势U,它的哈密顿量表示如下:
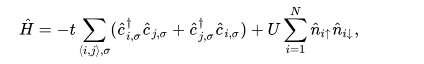
这个模型,求解大系统的精确解是不可能的,原理同上,因此如果要想求解基态,我们可以用下面的方法来做
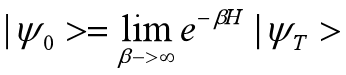
这里,右边代表的试探波函数,原理很简单,随着β的增加,基态由于能量最低,所占的比重越来越大,当趋近于无穷时,其他激发态的比重可以忽略不计,从而基态"脱颖而出"。
当然,我们实际上,需要把propagator拆成一小块一小块,然后对每一小块,都会有random walking,否则我们根本无法计算。最后的结果就是下式。
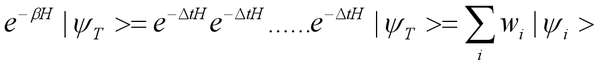
这里的i代表着walker的编号,如果我们想提高计算精度,就需要增大walker的数目。
最后我们计算基态能量,可以用如下的式子进行计算。
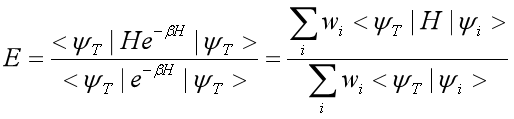
当然,如果求解某格点的自旋什么的,需要做back propagation,不能套用上面的式子。
这里的w(i)再乘上|φ(i)>与试探波函数的overlap对应着第i个walker的权重,当然实际上可能因为算法不同而有所变化。然而,因为费米子波函数的反对称性,只要不是半满填充,对于基态里任意一个|φ>,我们都能找到-|φ>,从而有
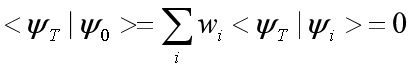
因此正负权重相抵,分母接近0,方差变的很大,实验结果惨不忍睹。
3,如何应对sign problem?
应对sign problem的方法有很多,一种典型的解决方法,也是我在做的,就是CPMC(Constrained path monte carlo)。方法就是,我们在做random walking的时候,要时刻监视每个walker权重的动向,一遇到负的权重,立刻斩草除根,就像下面这张图一样。下面的图, 左边是负权重,右边是正权重,我们让random walking待在正权重的区域。
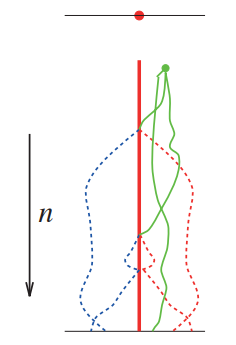
然而,我们并不知道基态(要是我们知道了还求它干什么),所以这个边界的划定就会出现问题。CPMC的做法,是让试探波函数充当"边界裁判",也就是舍弃掉和试探波函数的overlap为负的情况。
这就带来了一个问题,和试探波函数的overlap为负,并不代表和基态的overlap权重也为负。因此,CPMC的做法会"误伤友军",从而带来系统偏差。
不过好在,这样的系统偏差,在小的系统和较小的排斥势U,小到可以忽略不计。所以CPMC在计算小模型和较小的排斥势U的时候,可以算的非常准,稍微大点的系统或者U,我们就需要用一个比较好的试探波函数了,如果试探波函数和基态接近,那就可以减少"误伤友军"的概率。这里我们可以用平均场理论的基态波函数作为试探波函数,或者用自洽迭代的方式,都可以提高计算的精度。用这种方法,在计算100个格点以内,U不大于8的模型,我们都能让能量误差控制在千分之一以内。
那么,能不能彻底解决sign problem?答案是不能,这个问题是NP-hardness problem。详情请见: https://arxiv.org/abs/cond-mat/0408370
虽然不能解决,但是我们可以通过各种方法来改善结果,只要能让误差控制在合理范围内,我们也能观测到很多有趣的现象,发现新世界。这就是QMC的魅力所在。
参考文献:
《Auxiliary-Field Quantum Monte Carlo for Correlated Electron Systems 》 by Shiwei Zhang,最后一张图的出处也在那里。
来源:知乎 www.zhihu.com
作者:
Super Mario 【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。
点击下载 此问题还有
2 个回答,查看全部。 延伸阅读:
水在临界点发生了什么? 拓扑学在物理研究中有哪些具体应用?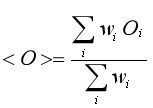
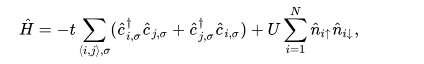
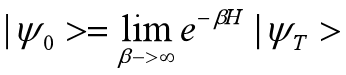
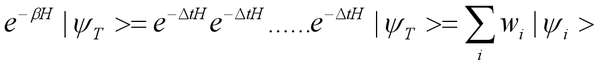
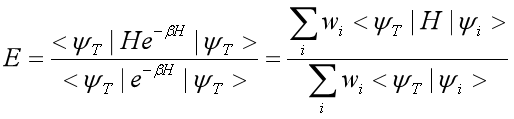
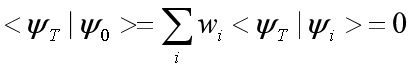

没有评论:
发表评论